Paradossi

Questo blog prende il titolo da un famoso paradosso di cui vi parlerò successivamente.
Per adesso risolvete questo se ci riuscite.

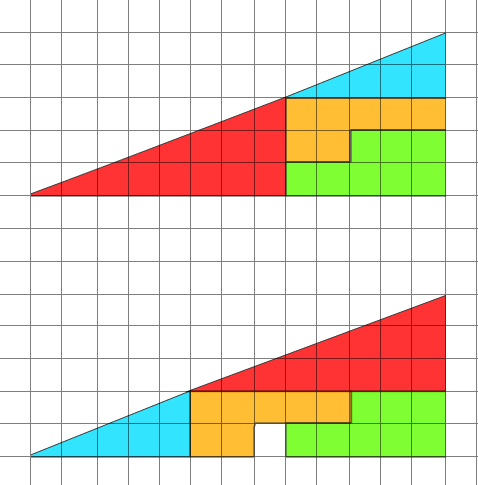
Qualcuno mi spiega come fanno questi due triangoli, composti dalle stesse parti semplicemente rimescolate ad avere area diversa?

Un aiuto ve lo do. Non è un paradosso ma un inganno. Non si devono mai confondere le due cose perchè sono concettualmente molto diverse tra loro. Un paradosso è un ragionamento apparentemente sensato, che partendo da premesse apparentemente sensate, giunge ad una conclusione apparentemente insensata o apparentemente in contrasto con le premesse. Più l'avverbio "apparentemente" della precedente definizione diminuisce di entità e più il paradosso diventa solido e interessante.
Un inganno invece è qualcosa la cui forma, per dolo, colpa o buonafede è diverso dalla sua sostanza. Per esempio una moneta falsa; appare identica ad una moneta vera ma non lo è.
Qualcuno dirà: "scusa ma vuoi parlare di paradossi e parti con un inganno?" si altrimenti che paradosso sarebbe?